About Me
My name is Reilly Browne and I am a PhD Student at Dartmouth College studying theoretical computer science under Prof. Hsien-Chih Chang.
I did my Bachelors and Masters at Stony Brook University, where I studied under Prof. Rezaul Chowdhury and Prof. Joseph Mitchell.
My primary focus has been working with problems in the interface of computational geometry and graph theory, particularly exploiting geometric structure to develop results for (generally) NP-hard problems. See the Theory Work tab for a list of my currently available papers, or look at my Google Scholar Profile.
Hobbies: Solving Puzzles (Rubik's Cube), Playing Irish Instruments, Creative Writing, Trivia, Game Development
Areas of Interest: Computational Geometry, Parallel Computing, Combinatorial Optimization, Geometric Graph Theory
Favorite Papers Titles: Hiding People in Polygons, Covering Polygons is Hard, Covering Polygons is Even Harder, Minimizing Movement,
Theory Work
Here is a collection of some papers I've written related to discrete and computational geometry. I hope to expand this list much more in the future as some works I plan on publishing, so they will appear here only after I get the go-ahead.Constant-Factor Approximation Algorithms for Convex Cover and Hidden Set in a Simple Polygon
In this paper, we give subcubic time approximation algorithms for convex cover and hidden set for simple polygons. This is the first constant factor approximation for both problems, and the first non-trivial approximation algorithm for hidden set that is known. Both problems have previously been proven to be APX-hard, so these algorithms imply they are in fact APX-complete. This paper is avalaible here and on Valentin's website
Convex Cover and Hidden Set in Funnel Polygons
In this paper, I give linear time algorithms for convex cover, hidden set, and hidden vertex set restricted to funnel polygons. From this, I am able to achieve 2-approximations for the same problems in pseudotriangles. I also give an example polygon where placing hidden points along the boundary of a pseudotriangle gives suboptimal solutions, implying that a very different method is required. This paper is also available on arxiv:
Cache-Oblivious Parallel Convex Hull in the Binary Forking Model
In this paper, I and other members of the SBU TEALab investigated the Convex Hull problem, specifically in 2D. We developed two parallel algorithms, one for presorted points and one for unsorted points, which achieve optimal cache complexity under the cache-oblivious model and optimal or state of the art span for the Binary Forking Model. This paper is also available on arxiv:
Collapsing the Hidden Set-Convex Cover Inequality
In this paper, I and my colleague Eric Chiu show a polygon for which hidden set and convex cover are declaratively distinct values and show two classes of polygons for which they are equivalent. The two classes also have linear time algorithms for finding both a hidden set and convex cover. This paper was accepted to CG Week's Young Researcher's Forum. Here is an extended version of the paper.
An Overview of Minimum Convex Cover and Maximum Hidden Set
In this survey paper, I collected all of my previous work on Convex Cover and Hidden Set into a single source. The full paper is available here
and on Arxiv.Polyhedral Nonexistence from Graphs
In this paper, inspired by coursework from Joseph S.B. Mitchell's Computational geometry class at SBU, I discuss some limitations on the existence of certain polyhedra using graph theory. The full paper is available here
and on Research Gate. Citation is available as BibTex here.My Other Projects
Here is a collection of other projects that I feature on my Github. For the full list of my repositories, go to my profile at https://github.com/Rajalo.Travelling Salesperson Tour Calculator
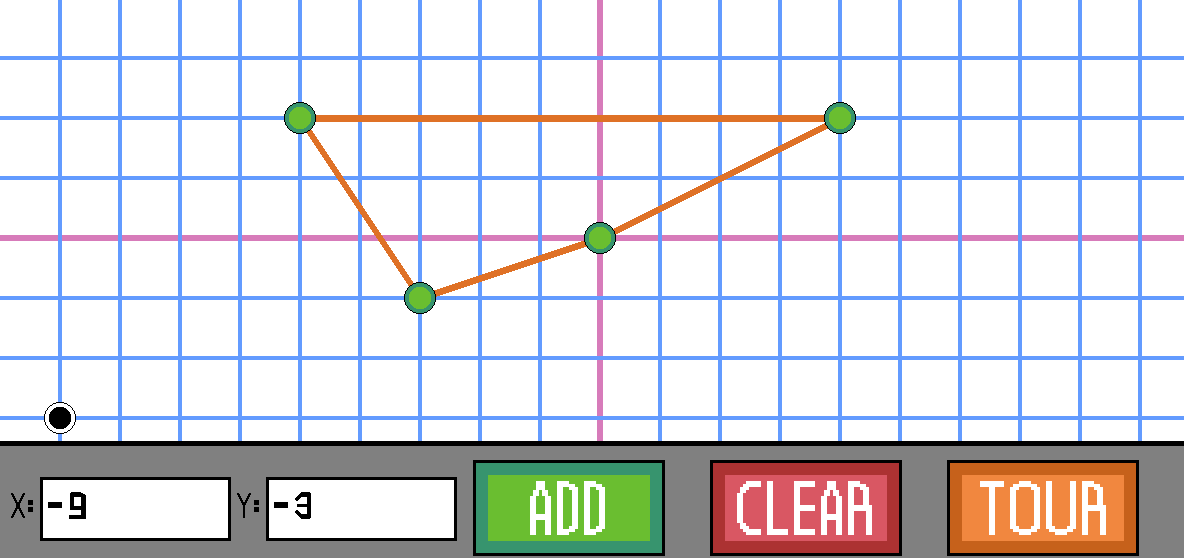
This program implements a branch and bound technique to find the optimal travelling salesperson tour for an inputted set of points. I wanted to give it a more retro feel, so I decided to do pixel art for every component, even the inputs for coordinates.
The program has a hard limit on the number of points that can be inputted, 20. It allows users to scroll vertically and horizontally through an infinite grid. The user can also add specific points using the coordinate input boxes.
To download, the release is here: https://github.com/Rajalo/TSPTourCalculator/releases/tag/v1.0
And the full repository is here https://github.com/Rajalo/TSPTourCalculator
Travelling Salesperson Approximations in Python
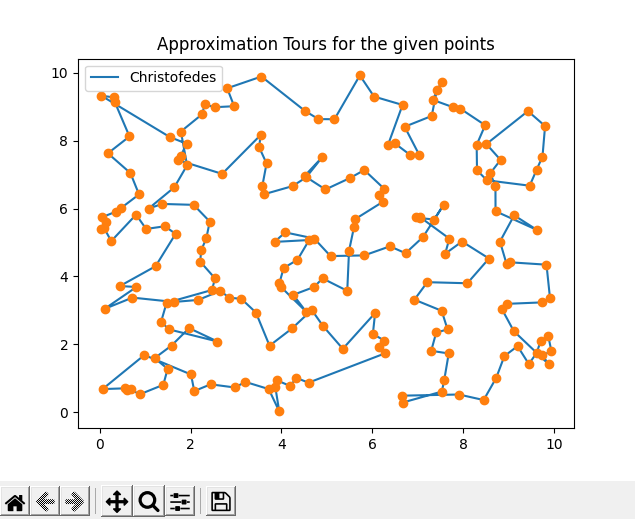
This repository is a collection of implementations of approximation algorithms for the optimal Travelling Salesperson tour for given points in the plane. I developed these implementations as part of a related research paper. Currently that paper is not complete, so I will link that here as well once that is finished.
The full repository is here https://github.com/Rajalo/TSP-Approximation-Algorithms-in-Python
Club Management Systems
This repository is a collection of Google Apps Script systems I made to help run clubs in high school and my freshman year of college. They automated some of the more mundane tasks of leadership, most centrally writing emails for notifying the membership of weekly goings-ons.
The full repository is here https://github.com/Rajalo/Club-Management-Systems
Dream Run

This is a game I made back in AP Computer Science. It's an arcade style game following a blue man's futile quest to get his jacket back from a flying trickster.
The full repository is here https://github.com/Rajalo/Dream-Run
RoseField Farms

This is a game I made my freshman year of college. It's an arcade style game following a farmer's attempts to keep a rose business afloat despite the shenanigans of local animals.
The full repository is here https://github.com/Rajalo/RoseField-Farms
Pixel Art Gallery
A fun hobby I've gotten into is game development. Often I like to sketch out my ideas for games by trying to create pixel art for the game to see how I like the idea. Here are some excerpts of that work. At the end I included the pixel art from my TSP Calculator, which is on my Github.
